Etapa de diagnóstico#
La etapa de diagnóstico del Ordenamiento Ecológico se refiere a la identificación de la aptitud sectorial y al análisis de los conflictos ambientales en el área de estudio. Así, el análisis de aptitud busca captar y representar la narrativa interna de cada sector, incorporando formalmente al análisis sus valores, necesidades y aspiraciones con respecto al uso del territorio.
Si quieres replicar el proceso de creación de índices de aptitud, descarga el manual
aquíSi quieres visualizar las capas geográficas que se utilizaron como insumos en esta etapa, da click en http://www.apc.lancis.ecologia.unam.mx/fomix/index.php/view/map/?repository=indices&project=insumos.
Si quieres visualizar los mapas resultado de los talleres participativos, da click en http://www.apc.lancis.ecologia.unam.mx/fomix/
A continuación, se exponen brevemente las principales herramientas analíticas utilizadas por el equipo técnico del LANCIS para elaborar índices y mapas de aptitud para la etapa de diagnóstico del Programa de Ordenamiento Ecológico del estado de Yucatán.
Proceso Analítico Jerárquico#
El Proceso Analítico Jerárquico (AHP, por sus siglas en inglés) es la representación de un problema de decisión en una estructura jerárquica. Esta técnica está fundamentada en la facilidad del cerebro humano para hacer comparaciones pareadas, es decir, que el usuario debe priorizar elementos de decisión de dos en dos. Este procedimiento simplifica la tarea de priorizar ordenadamente cada elemento entre múltiples opciones. La estructura general de un modelo AHP consiste en tres niveles organizados: la meta como primer nivel, los criterios como segundo y las alternativas de decisión como tercero. El usuario puede desagregar los criterios (es decir, desarrollar subcriterios) tanto como crea conveniente, lo cual resulta en más de tres niveles de desagregación.
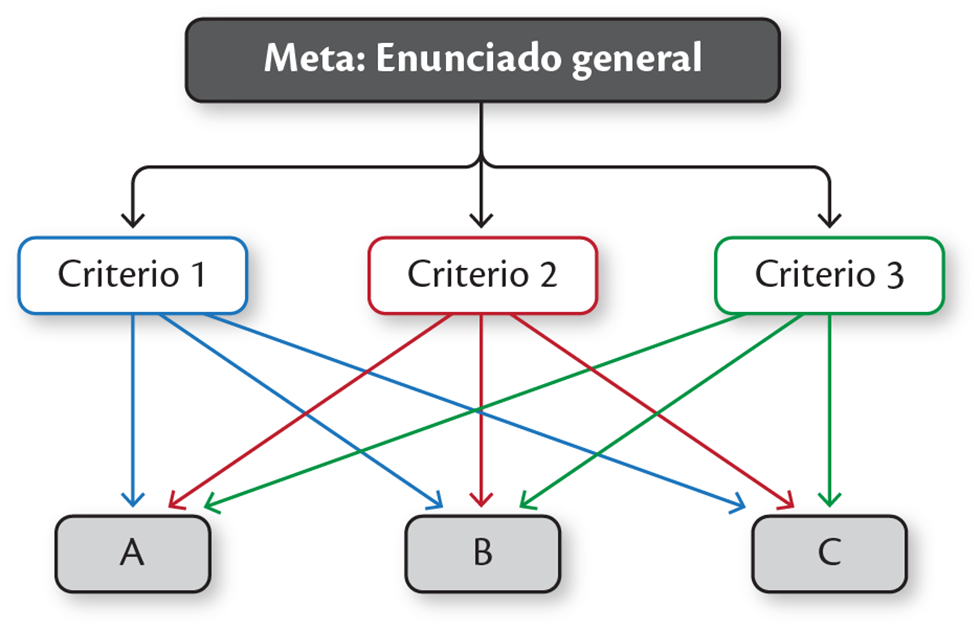
Estructura general del AHP#
Si quieres saber más sobre el AHP, descarga el manual
aquíEn el manual encontrarás un ejemplo desarrollado en Excel que puedes descargar
aquíCada hoja del archivo Excel corresponde a una estructura jerárquica de número de criterios de decisión creciente.Si quieres usar un software específico para modelación multicriterio visita la página de SuperDecisions (https://www.superdecisions.com/downloads/).
Referencias
Eakin, H. y L. A. Bojórquez-Tapia. (2008). “Insights into the Composition of Household Vulnerability from Multicriteria Decision Analysis.” Global Environmental Change. https://doi.org/10.1016/j.gloenvocha.2007.09.001
Merino, T., Grave, I., & Bojórquez-Tapia, L. A. (2020). Ahp-Based Social Vulnerability Index for Small Fisheries in Yucatan, Mexico. 2, 1–5. https://doi.org/10.13033/isahp.y2020.010
Saaty, R. W. (1987). “THE ANALYTIC HIERARCHY PROCESS-WHAT AND HOW IT IS USED” 9 (3): 161–76.
Saaty, T. L. (1996). Decision Making with Dependence and Feedback: The Analytic Network Process. In RWS Publications, 1996, ISBN 0-9620317-9-8. http://www.rwspublications.com/books/anp/decision-making-with-dependence-and-feedback/(Saaty, 1996)
Funciones de valor#
Las funciones de valor son expresiones matemáticas que se utilizan para transformar los valores de un criterio de decisión a una escala de medición de 0 a 1. En esta escala, 0 representa el estado anti-ideal (menos deseable) y 1 representa el ideal (más deseable). Es a través de las funciones de valor que es posible transformar dos mediciones en unidades diferentes a una unidad común. Existen dos tipos generales de funciones de valor: nominales y continuas. Las funciones de valor nominales se usan para representar los diferentes estados de criterios definidos por nombres; por ejemplo, tipo de vegetación o tipo de suelo. Este tipo de funciones se generan mediante métodos de modelación multicriterio como el AHP.Las funciones de valor continuas se usan para representar criterios definidos por variables continuas; por ejemplo, temperatura y precipitación. A su vez, las funciones de valor continuas se clasifican en términos de su comportamiento en: crecientes, decrecientes, óptimas y logísticas.
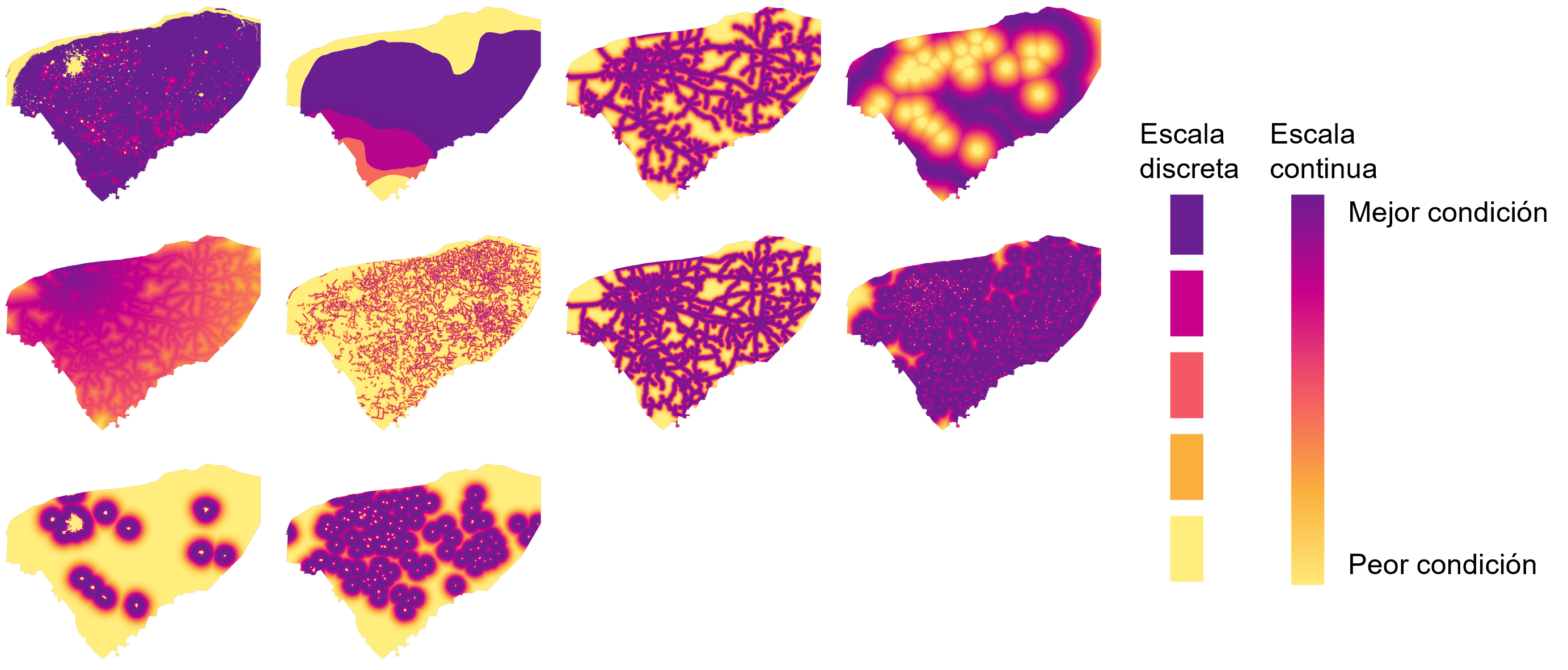
Ejemplo de funciones de valor discretas y continuas en capas geográficas#
Si quieres saber más sobre las funciones de valor continuas, descarga el manual
aquíEn el manual encontrarás ejemplos desarrollados en Excel, los cuales puedes descargar
aquíSi buscas diseñar de manera interactiva funciones de valor continuas, visita nuestra aplicación en línea: http://www.apc.lancis.ecologia.unam.mx:8053/
Referencias
Beinat, E. (1997). “Value functions for environmental management”. En: Value Functions for Environmental Management, Environment & Management, vol. 7. Springer, Dordrecht. https://doi.org/10.1007/978-94-015-8885-0_4
Bausch, J. C.,Bojórquez-Tapia, L., y Eakin, H. (2014). “Agro-environmental sustainability assessment using multicriteria decision analysis and system analysis”. Sustainability Science, 9: 303-319. doi: 10.1007/s11625-014-0243-y
Merino-Benítez, T., Hernández, V., Grave, I., y Bojórquez-Tapia, L.A. (2022). Finding Optimal Infrastructure Invest-ments with GIS-MCDA, Proceedings of the International Symposium on the Analytic Hierarchy Process: the 17th ISAHP conference, DOI: https://doi.org/10.13033/isahp.y2022.042
Saaty, R. W. (1987). “The analytic hierarchy process-what and how it is used”. Mathl Modelling, 9(3): 161–176.
Ley de Weber-Fechner#
La ley de Weber-Fechner es el precepto de la psicofísica que establece la relación logarítmica entre la magnitud de un estímulo y la intensidad de su percepción. Es decir, esta ley corresponde a utilizar el conocimiento de las respuestas psicológicas de las personas a la variación de un estímulo físico para definir los rangos de datos apropiados que determinen una categoría. Esta ley afirma que un cambio en la magnitud de estímulo se puede notar solo después de que aumenta en un porcentaje constante, llamado «diferencia apenas perceptible» (just noticeable difference, por su nombre en inglés). Esto significa que mientras que la magnitud de un estímulo varía en progresión geométrica, la percepción de su intensidad varía en progresión aritmética. La relación entre el cambio de intensidad y el estímulo de es una constante llamada «Factor de Progresión» (FP).
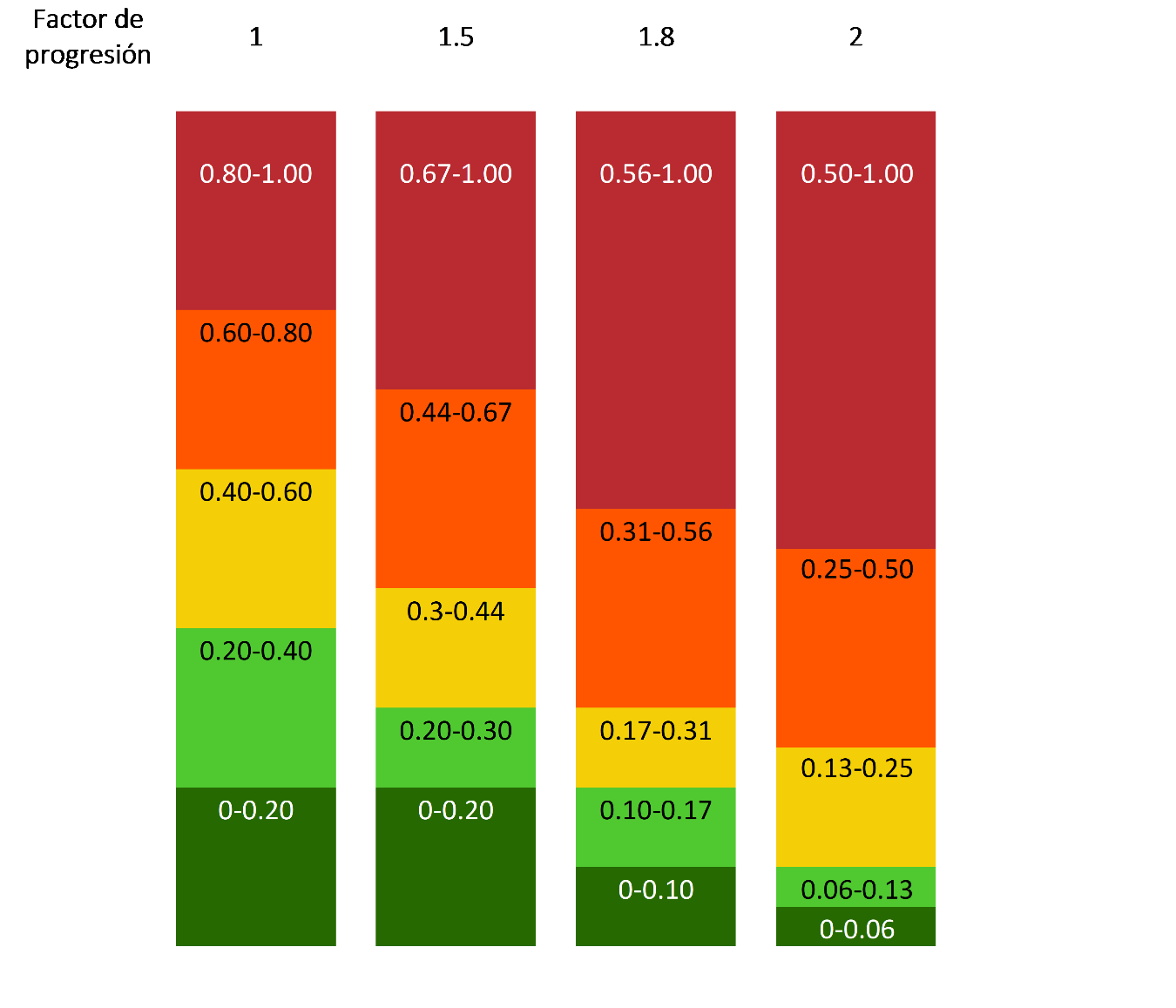
Cortes de una escala con diferentes FP#
Si quieres calcular cortes de escalas utilizando la Ley de Weber-Fechner, descarga
aquíel archivo en Excel que te permite variar el número de categorías que deseas obtener, así como el FP, y graficar la escala resultante.Si buscas categorizar un conjunto de datos de manera interactiva, puedes visitar nuestra aplicación en línea: http://www.apc.lancis.ecologia.unam.mx:8051/
Referencias
Bojórquez-Tapia, L. A., Cruz-Bello, G. M., y Luna-González, L. (2013). «Connotative land degradation mapping: A knowledge-based approach to land degradation assessment». Environmental Modelling and Software, 40, 51–64. https://doi.org/10.1016/j.envsoft.2012.07.009
Lootsma, F. A. (1999). «Multi-Criteria Decision Analysis via Ratio and Difference Judgement Applicd Optimization». In Optimization.
Media Ordenada Ponderada#
La Media Ordenada Ponderada (OWA, Ordered Weighted Average) es un operador de evaluación multicriterio que permite generar una serie de escenarios de aptitud territorial a partir de «cuantificadores lingüísticos difusos» (enunciados que estiman medidas de manera ambigua o imprecisa: por ejemplo, “casi 10”, “cerca de 5”, etcétera). OWA permite generalizar métodos de evaluación multicriterio que consideran reglas de combinación no compensatorias (booleanas) y compensatorias (como la Combinación Lineal Ponderada) Su uso permite visualizar geográficamente la influencia de las estrategias de manejo ambiental.
Una ventaja del operador OWA es que posibilita la exploración de distintas actitudes respecto a la aptitud del territorio. En general, la actitud optimista tiene una propensión de tomar riesgos y, por lo tanto, enfatizan las buenas propiedades de una ubicación. Por el contrario, las actitudes pesimistas se inclinan hacia la aversión al riesgo y, por lo tanto, enfatizan las malas propiedades de una ubicación. En OWA, estas actitudes varían en un continuo en cuyos extremos se encuentran los operadores booleanos Y (MIN), del lado pesimista, y O (MAX), del lado optimista.
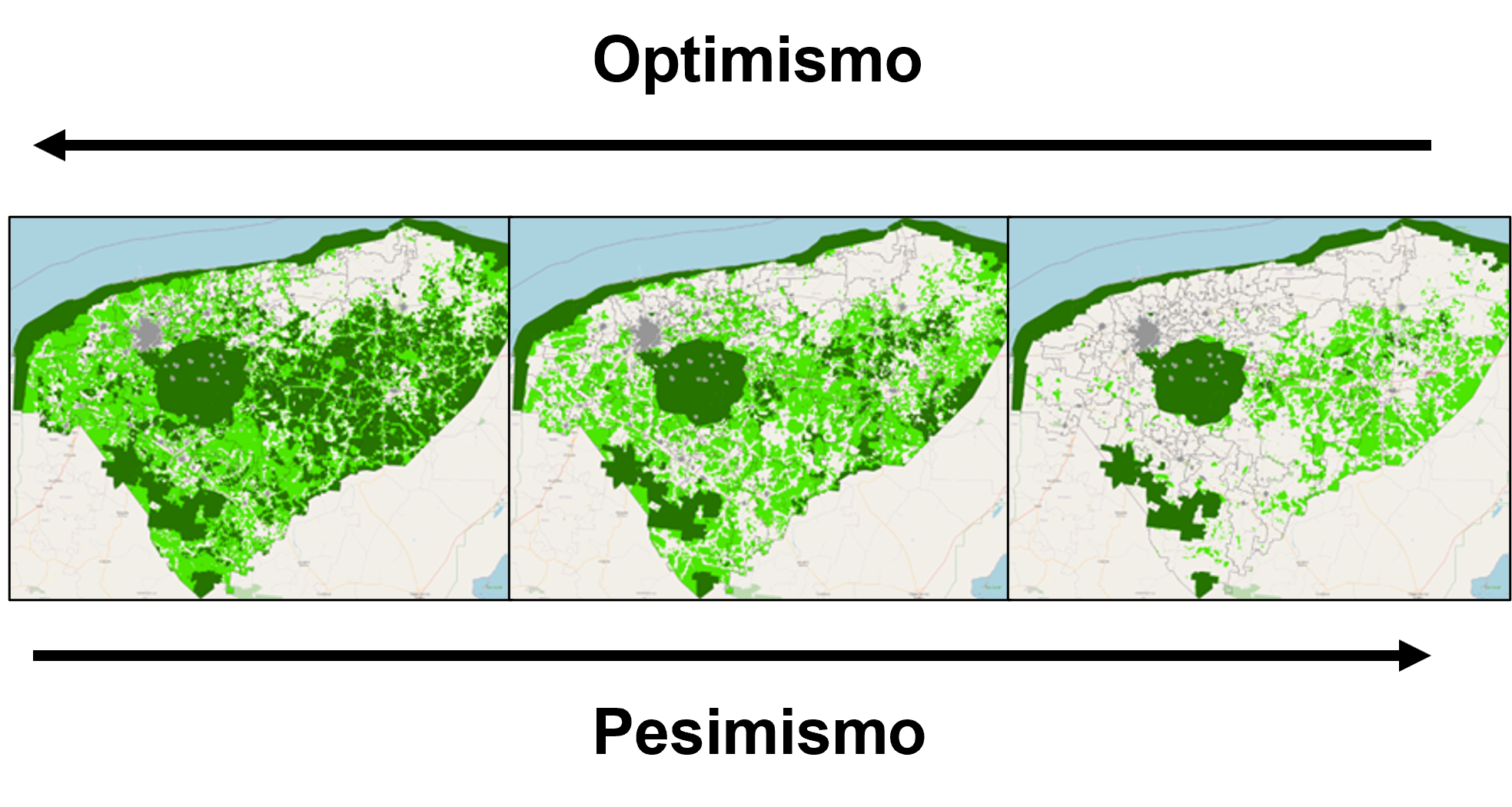
Ejemplo de escenarios de aptitud territorial con OWA#
Si quieres conocer más sobre OWA, descarga el manual
aquíSi quieres utilizar el algoritmo OWA para análisis geoespaciales, ve al siguiente enlace: https://lancis-apc.github.io/geo_lancis/owa.html
Referencias
Malczewski, J. 2004. GIS-based land-use suitability analysis: A critical overview. Progress in Planning,62(1), 3–65. https://doi.org/10.1016/j.progress.2003.09.002
Malczewski, J. 2006. Ordered weighted averaging with fuzzy quantifiers: GIS-based multicriteria evaluation for land-use suitability analysis. International Journal of Applied Earth Observation and Geoinformation, 8(4), 270–277. https://doi.org/10.1016/j.jag.2006.01.003
Malczewski, J. y C. Rinner. 2015. Multicriteria Decision Analysis in Geographic Information Science. Analysis methods. https://doi.org/10.1007/978-3-540-74757-4
Merino-Benítez, T., Hernández, V., Grave, I., y Bojórquez-Tapia, L.A. (2022). Finding Optimal Infrastructure Invest-ments with GIS-MCDA, Proceedings of the International Symposium on the Analytic Hierarchy Process: the 17th ISAHP conference, DOI: https://doi.org/10.13033/isahp.y2022.042
